Definition of Orbital
Orbital in chemistry or physics defines a three-dimensional region where the probability of finding an electron is maximum. The wave function suggests that the probability of finding an electron in three-dimensional space around the nucleus involves two aspects, radial probability, and angular probability. The pictorial representation of an orbital in two-dimensional space is difficult. It is generally represented by a shaded picture in which the intensity of shading is proportional to the portability of finding the electron at that location.
- The square of the radial part of the wave function indicates the probability of finding the electron at any distance r from the nucleus.
- The square of the angular part of the wave function gives the probability of finding an electron in a particular direction from the nucleus.
- If the radial and angular dependence of wave function is taken together, it defines the three-dimensional standing electron wave or cloud or orbital which predicts the size shape, and orientation of atomic orbitals.
Quantum Number Orbital Diagram
In order to describe the size, shape, and orientation of the orbital, three quantum number is necessary. These quantum numbers are
- Principal (n) quantum number
- Azimuthal quantum number (l)
- Magnetic quantum number (m)
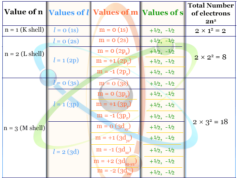
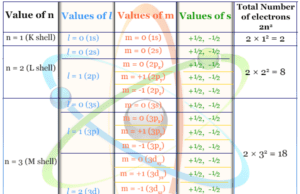
In the study chemistry, the relation between quantum number and orbital designation is represented in the below table.
| Principal quantum number (n) | Azimuthal quantum number (l) | Magnetic quantum number (m) |
| n=1 (K-shell) |
l = 0 (1s) | m = 0 (2s) |
| n = 2 L-shell |
l = 0 (2s) | |
| l = 1 (2p) | m = 0 (2px) | |
| m = +1 (2py) | ||
| m = −1 (2pz) | ||
| n =3 M-shell |
l = 0 (3s) | m = 0 (3s) |
| l = 1 (3p) | m = 0 (3px) | |
| m = +1 (3py) | ||
| m = −1 (2pz) | ||
| l = 2 (3d) | m = 0 (3dxy) | |
| m = +1 (3dyz) | ||
| m = −1 (3dxz) | ||
| m = +2 (3dx2-y2) | ||
| m = −2 (3dz2) |
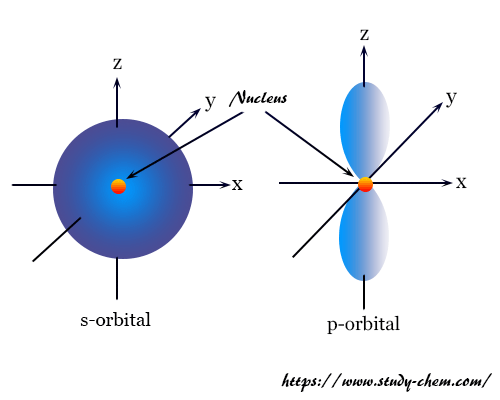
Shape of s-orbital
From the above table, we have seen that for s-orbitals l = 0 and m = 0. It indicates that the s-orbital has only one orientation in space with a spherically symmetrical shape.
The electron cloud density in s-orbitals is not concentrated in any particular direction. Therefore, an equal chance of finding the electron density in any direction with respect to the nucleus of an atom.
Shape of p-orbitals
For p-orbital l = 1 and m = +1, 0, −1. Three values of magnetic quantum number (m) define the three orientations along the x, y, and directions. Therefore, p-orbitals are designated as px, py, and pz.
In the absence of a magnetic or electric field, these three orbitals are equivalent in energy. Therefore, they are said to be three-fold degenerate or triply degenerate energy levels.
The three p-orbitals are dumb-bell shapes which is perpendicular to each other. Each of the three p-orbitals has two lobes touching each other at the origin. These lobes are completely symmetrical along any of the three axes. For example, the px-orbital is symmetrical to the x-axis.
The plane which separates the two lobes of the p-orbital is called the nodal plane. The electron density on the nodal plane is zero. For px-orbital, yz-plane is the nodal plane.
Shape of d-orbitals
d-orbital arises when n = 3 and m = +2, +1, 0, −2, −1 or it starts with the 3rd main energy level. The azimuthal quantum number indicates that d-orbitals have five orientations in space.
Five orientations along the x, y, and z-axis are named dxy, dxz, dyz, dx2-y2, and dz2.
- The three orbitals namely dxy, dyz and dxz have their lobes lying symmetrically between their respective coordinate axis. For example, the lobes of the dxy orbital lie between the x and y-axis. This set of three orbitals is known as the t2g set non-axial set.
- The lobes of dx2-y2 are lying along the x and y-axis and the lobes of dz2 are lying along the z-axis. This set of two orbitals is called eg set or axial set.